aula-4 – Caderno de aulas

GLM, ANOVA Fatorial e Interações: Aplicações Práticas no R

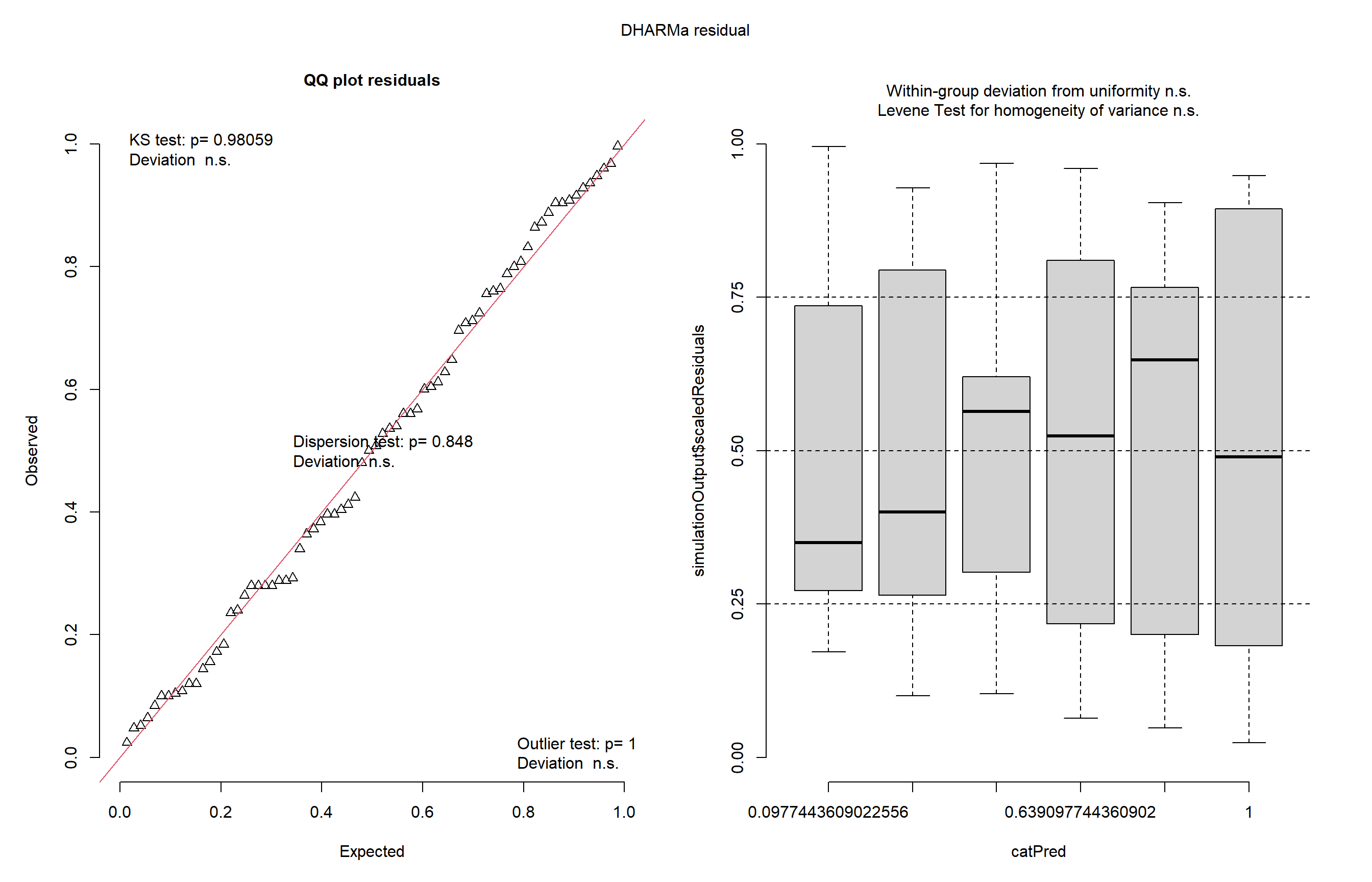
Nesta aula, vamos aprofundar a análise estatística utilizando modelos mais robustos e flexíveis, como o modelo linear generalizado (GLM), a ANOVA fatorial e a análise de interações entre fatores.

Para isso, vamos retomar os dados da aula anterior (InsectSprays) e aplicar um modelo GLM com distribuição Poisson para contagens. Além disso, utilizaremos a ferramenta DHARMa para diagnóstico gráfico com resíduos simulados.

Diagnóstico com resíduos simulados (DHARMa)

DHARMa é uma ferramenta poderosa que substitui os métodos tradicionais de diagnóstico (como apenas shapiro.test() e gráficos QQ-plot) por uma abordagem mais robusta, principalmente quando saímos da ANOVA clássica e entramos em modelos transformados ou GLMs.

library(DHARMa)
insetos <- InsectSprays
m3 <- lm(rank(count) ~spray, data = insetos)
plot(simulateResiduals(m3))

Após verificarmos a adequação do modelo transformado com o auxílio do pacote DHARMa, agora vamos explorar uma abordagem alternativa utilizando um modelo de regressão generalizada (GLM) com distribuição Poisson, que é especialmente indicado para dados de contagem como os presentes no conjunto InsectSprays.

Modelo de regressão linear generalizada (GLM) c com distribuição Poisson

A função glm() pertence ao pacote base do R e é usada para ajustar modelos lineares generalizados. Essa função permite modelar diferentes tipos de variáveis resposta (contagem, proporção, binária, etc.) por meio da especificação de uma família de distribuição e uma função de ligação (link function).

Neste caso, vamos usar a família poisson, que é apropriada para dados de contagem.

m4 <- glm(count ~ spray, data = insetos,
          family = poisson)

Após ajustar o modelo com glm(), precisamos avaliar se o fator spray tem efeito significativo sobre a variável resposta. Para isso, faremos uma análise de deviance, que é o equivalente da ANOVA nos modelos GLM.

Avaliação do modelo

Análise de deviance sequencial com anova()

Realiza uma análise de deviance sequencial (Type I) do modelo GLM, mostrando se os fatores incluídos influenciam significativamente a variável resposta.

anova(m4)

Analysis of Deviance Table

Model: poisson, link: log

Response: count

Terms added sequentially (first to last)

      Df Deviance Resid. Df Resid. Dev  Pr(>Chi)    
NULL                     71     409.04              
spray  5   310.71        66      98.33 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Análise de Deviance Tipo II com Anova() do pacote car

Essa função é uma versão mais robusta da análise de variância, que permite testar efeitos de forma mais detalhada, incluindo correções para diferentes tipos de desequilíbrios nos dados.

library(car)
Anova(m4)

Analysis of Deviance Table (Type II tests)

Response: count
      LR Chisq Df Pr(>Chisq)    
spray   310.71  5  < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Verificação Automática das Premissas com check_model()

library(performance)
check_model(m4)

Diagnóstico de Resíduos Simulados com plot(simulateResiduals())

plot(simulateResiduals(m4))

O modelo de regressão de Poisson ajustado mostrou que o fator spray tem efeito altamente significativo sobre a variável resposta com o valor de p < 0,05. Agora usaremos emmeans para descobrir onde exatamente estão essas diferenças.

Comparações múltiplas com `emmeans` e `cld`

library(emmeans)
library(multcomp)
medias_m4 <- emmeans(m4, ~spray, type = "response")
cld(medias_m4)

 spray  rate    SE  df asymp.LCL asymp.UCL .group
 C      2.08 0.417 Inf      1.41      3.08  1    
 E      3.50 0.540 Inf      2.59      4.74  12   
 D      4.92 0.640 Inf      3.81      6.35   2   
 A     14.50 1.100 Inf     12.50     16.82    3  
 B     15.33 1.130 Inf     13.27     17.72    3  
 F     16.67 1.180 Inf     14.51     19.14    3  

Confidence level used: 0.95 
Intervals are back-transformed from the log scale 
P value adjustment: tukey method for comparing a family of 6 estimates 
Tests are performed on the log scale 
significance level used: alpha = 0.05 
NOTE: If two or more means share the same grouping symbol,
      then we cannot show them to be different.
      But we also did not show them to be the same.

A comparação múltipla das médias ajustadas pelo modelo de Poisson, com correção de Tukey, revelou diferenças significativas entre alguns tratamentos com spray. A análise indicou que o tratamento C teve a menor média de contagem (2,08) e diferiu significativamente dos demais. Os tratamentos E (3,50) e D (4,92) apresentaram médias intermediárias. Já os tratamentos A (14,50), B (15,33) e F (16,67) tiveram as maiores médias e não diferiram entre si, formando um grupo estatisticamente semelhante.

Anova fatorial

Essa análise é utilizada quando se deseja avaliar simultaneamente o efeito de dois ou mais fatores sobre uma variável resposta e investigar se existe interação entre esses fatores. Usaremos para demonstração o conjunto de dados antifungicos, disponível online, que contém informações sobre a severidade de uma doença fúngica sob diferentes tratamentos e doses aplicadas.

library(gsheet)
antifungicos <- gsheet2tbl("https://docs.google.com/spreadsheets/d/1bq2N19DcZdtax2fQW9OHSGMR0X2__Z9T/edit?gid=2023059672#gid=2023059672")
View(antifungicos)

Antes da análise estatística, vamos visualizar os dados em um três gráficos de dispersão com pontos usando geom_jitter():

Gráfico de dispersão por dose e tratamento:

library(tidyverse)
antifungicos |> 
  ggplot(aes(dose, severity*100))+
  geom_jitter(width = 0.1)+
  facet_wrap(~ treat)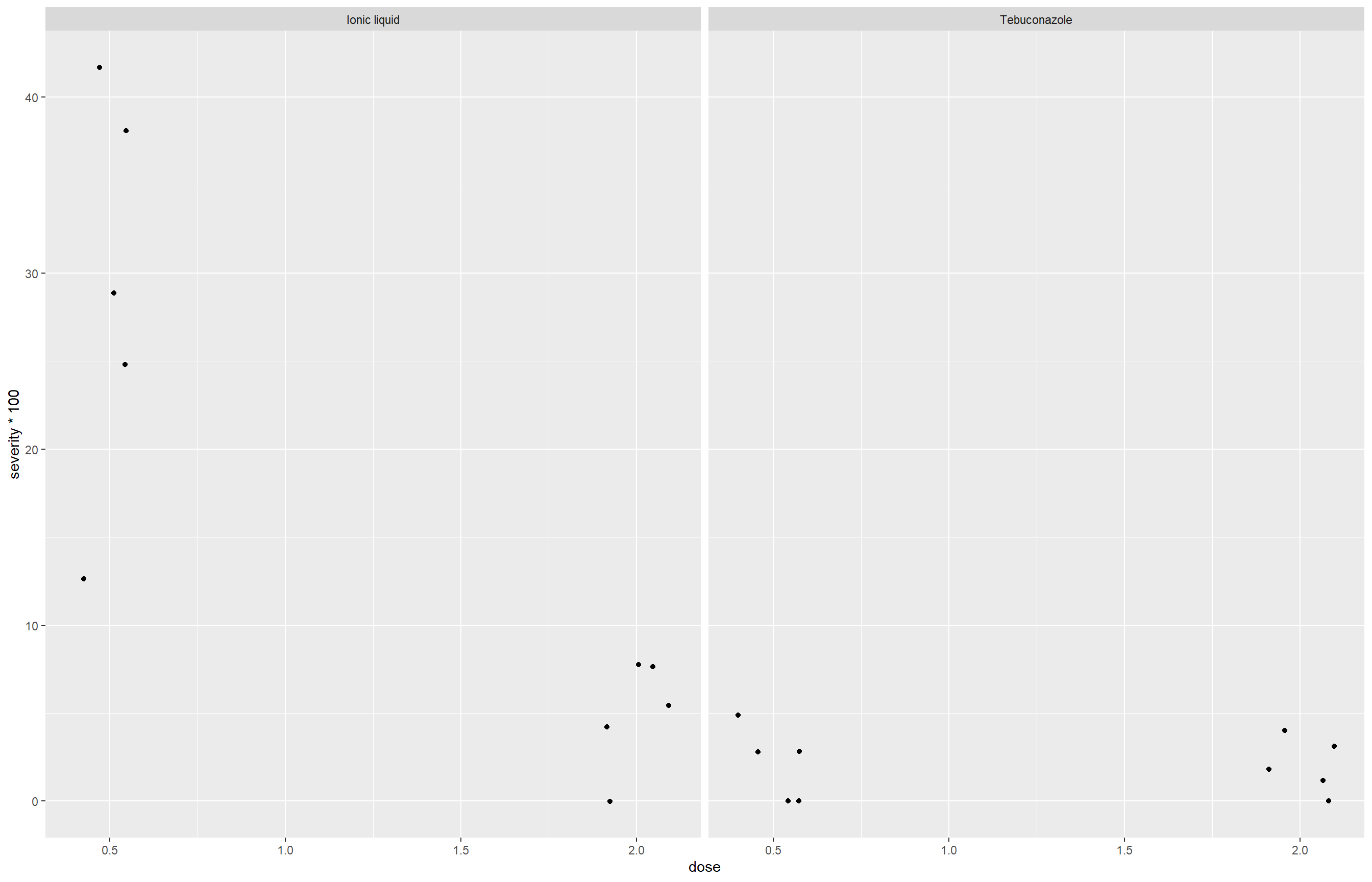

Gráfico de interação:

interaction.plot(antifungicos$dose, antifungicos$treat,
                 antifungicos$severity)

Esse gráfico ajuda a visualizar a possível interação entre os fatores dose e treat.

Gráficos separados por fator (para comparação individual):

p1 <- antifungicos |> 
  ggplot(aes(factor(dose), severity*100))+
  geom_jitter(width = 0.1)

p2 <- antifungicos |> 
  ggplot(aes(treat, severity*100))+
  geom_jitter(width = 0.1)
library(patchwork)
p1+p2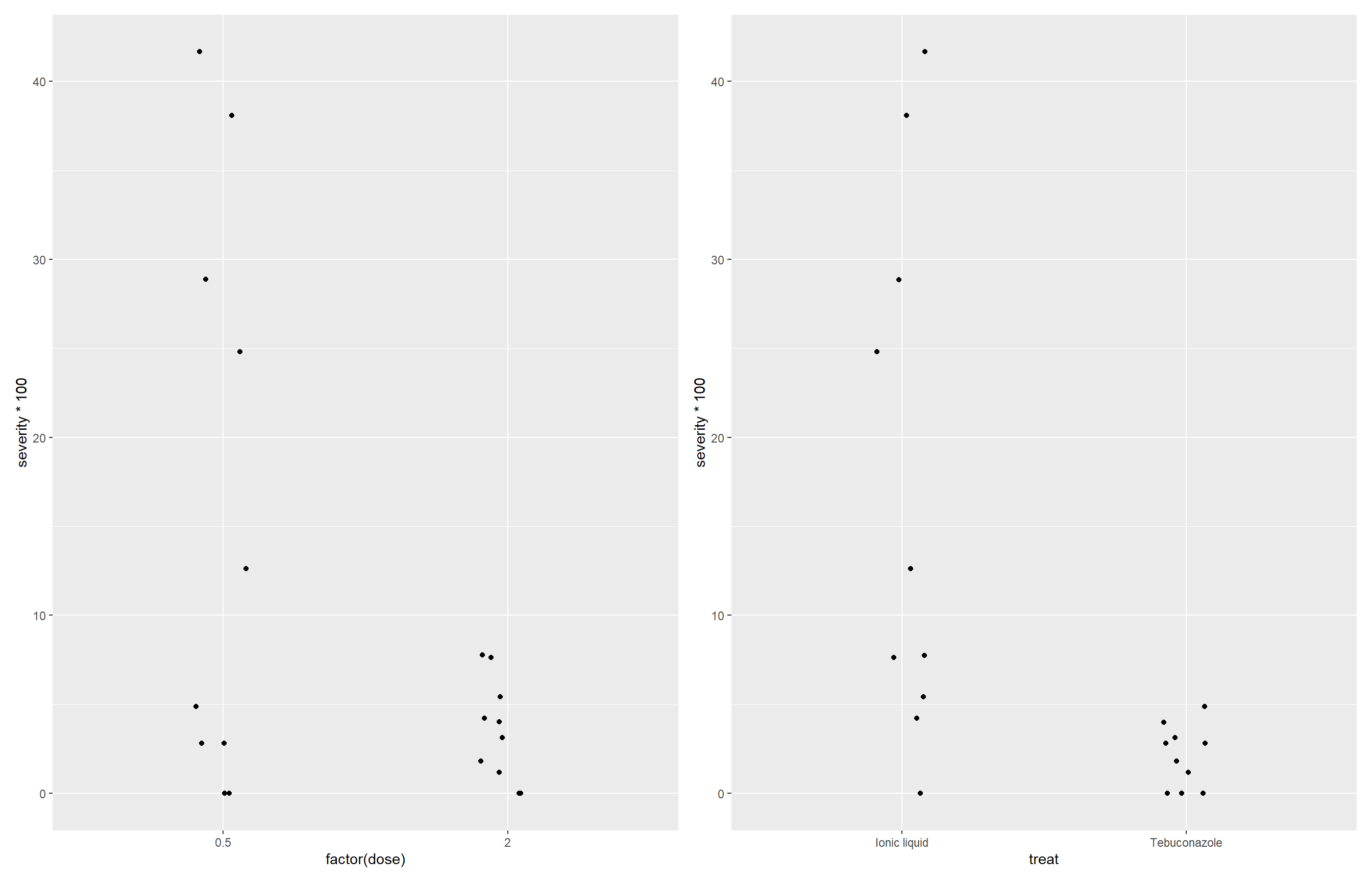

O uso do patchwork permite colocar os dois gráficos lado a lado para facilitar a comparação visual entre os fatores.

Ajuste do modelo linear com interação

m_anti <- lm(severity ~ treat*dose, data = antifungicos)

Análise de variância (ANOVA) do modelo ajustado

anova(m_anti)

Analysis of Variance Table

Response: severity
           Df   Sum Sq  Mean Sq F value    Pr(>F)    
treat       1 0.113232 0.113232  30.358 4.754e-05 ***
dose        1 0.073683 0.073683  19.755 0.0004077 ***
treat:dose  1 0.072739 0.072739  19.502 0.0004326 ***
Residuals  16 0.059678 0.003730                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

O valor de p para a interação foi significativo (p < 0,05), isso indica que o efeito da dose depende do tratamento utilizado (e vice-versa).

Seguiremos com a verificação das premissas do modelo, garantindo que os pressupostos da ANOVA estejam sendo atendidos.

Avaliação do modelo

plot(simulateResiduals(m_anti))

Comparações múltiplas com `emmeans` e `cld`

media_anti <- emmeans(m_anti, ~ dose | treat )
media_anti

treat = Ionic liquid:
 dose emmean     SE df lower.CL upper.CL
  0.5 0.2921 0.0273 16  0.23420   0.3500
  2.0 0.0501 0.0273 16 -0.00781   0.1080

treat = Tebuconazole:
 dose emmean     SE df lower.CL upper.CL
  0.5 0.0210 0.0273 16 -0.03690   0.0789
  2.0 0.0202 0.0273 16 -0.03768   0.0781

Confidence level used: 0.95

cld(media_anti)

treat = Ionic liquid:
 dose emmean     SE df lower.CL upper.CL .group
  2.0 0.0501 0.0273 16 -0.00781   0.1080  1    
  0.5 0.2921 0.0273 16  0.23420   0.3500   2   

treat = Tebuconazole:
 dose emmean     SE df lower.CL upper.CL .group
  2.0 0.0202 0.0273 16 -0.03768   0.0781  1    
  0.5 0.0210 0.0273 16 -0.03690   0.0789  1    

Confidence level used: 0.95 
significance level used: alpha = 0.05 
NOTE: If two or more means share the same grouping symbol,
      then we cannot show them to be different.
      But we also did not show them to be the same.

As comparações múltiplas das médias ajustadas mostram que, no tratamento com Ionic liquid, há diferença significativa entre as doses: a dose de 0,5 apresentou severidade média significativamente maior que a dose de 2,0. Já no tratamento com Tebuconazole, as duas doses (0,5 e 2,0) não diferem estatisticamente entre si, pois compartilham o mesmo grupo na letra de agrupamento (.group = 1).

Esses resultados indicam que o efeito da dose na severidade da doença depende do tipo de tratamento utilizado, reforçando o efeito de interação entre dose e tratamento, como apontado anteriormente na ANOVA fatorial.

Avaliação da precisão do modelo

Por fim, avaliamos a precisão do experimento utilizando o coeficiente de variação (CV), com a função cv.model() do pacote agricolae:

library(agricolae)
cv.model(m_anti)

[1] 63.7165

O valor de CV (coeficiente de variação) calculado com cv.model(m_anti) foi de 63,72%, o que indica alta variabilidade residual em relação à média do experimento.

Análise de severidade da doença (OIDIO) com interação entre fatores

Nesta etapa, vamos utilizar o conjunto de dados PowderyMildew do pacote epifitter, que contém informações sobre a progressão da severidade da doença em diferentes tipos de irrigação e níveis de umidade.

Primeiramente, filtramos os dados para incluir apenas os sistemas de irrigação de interesse:

library(epifitter)
oidio <- PowderyMildew
oidio2 <- oidio |> 
  dplyr::filter(irrigation_type %in% c
         ("MS", "MS above canopy", "Overhead"))

Em seguida, visualizamos graficamente a evolução da severidade (sev) ao longo do tempo, estratificada por tipo de irrigação e umidade:

ggplot(oidio2, aes(time, sev))+
  geom_point()+
  facet_grid(moisture ~ irrigation_type)

Para quantificar a severidade acumulada da doença, calculamos a Área Abaixo da Curva de Progresso da Doença (AUDPC) por bloco, tipo de irrigação e umidade:

oidio3 <- oidio2 |>
  dplyr::group_by(irrigation_type, moisture, block) |>
  dplyr::summarize(AUDPC = AUDPC(time, sev))

Visualizamos os dados de AUDPC:

oidio3 |>
  ggplot(aes(irrigation_type, AUDPC, color = moisture))+
  geom_point(size = 2)+
  scale_y_continuous(limits = c(0,20))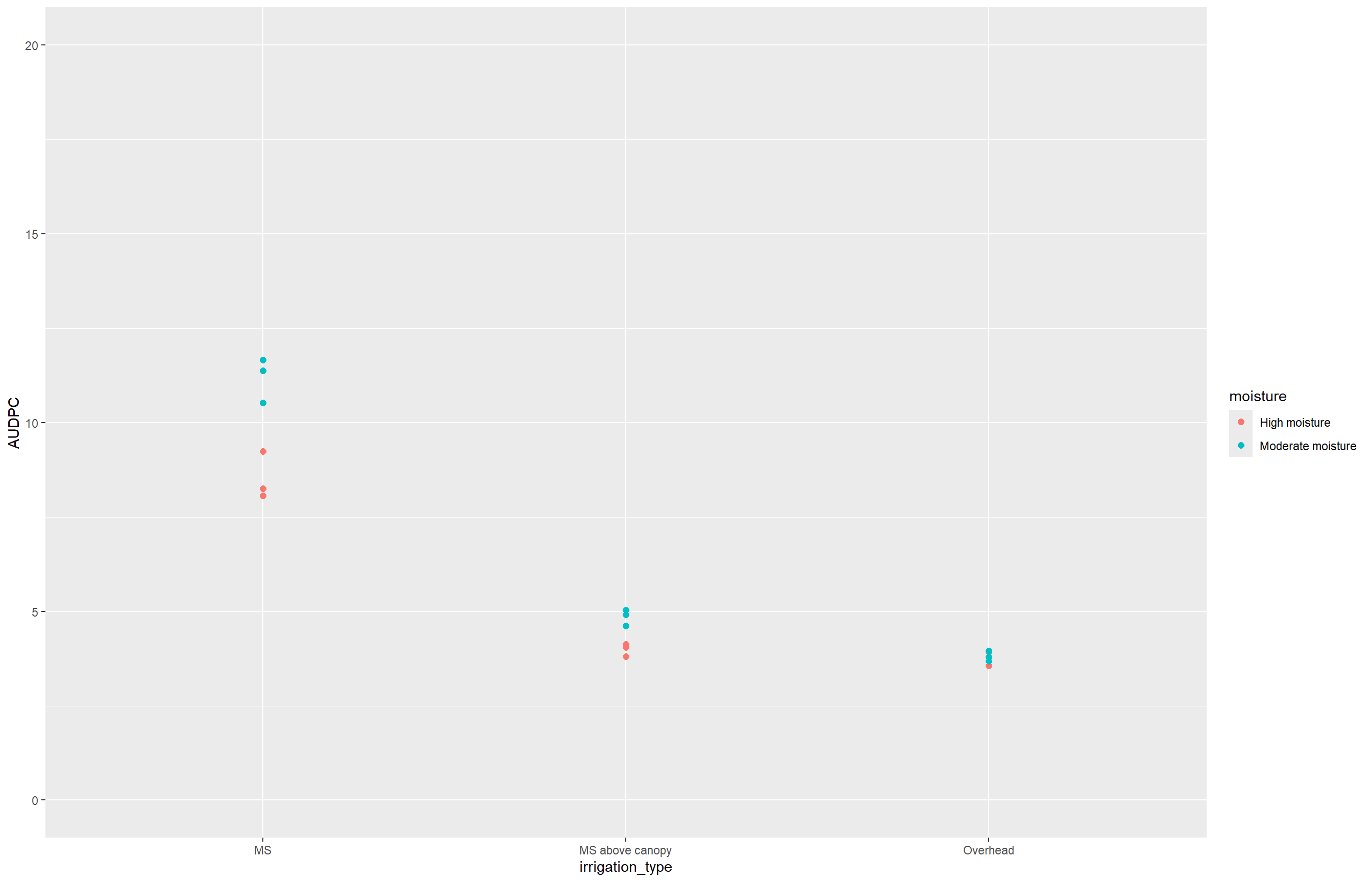

Modelo linear com interação

Ajustamos um modelo linear com interação entre os fatores irrigation_type e moisture para investigar se esses fatores afetam significativamente a severidade acumulada da doença:

model_oidio <- lm(AUDPC ~ irrigation_type * moisture,
                  data = oidio3)
anova(model_oidio)

Analysis of Variance Table

Response: AUDPC
                         Df  Sum Sq Mean Sq F value    Pr(>F)    
irrigation_type           2 134.341  67.170 451.721 5.073e-12 ***
moisture                  1   6.680   6.680  44.924 2.188e-05 ***
irrigation_type:moisture  2   5.104   2.552  17.162 0.0003022 ***
Residuals                12   1.784   0.149                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

revelou que os fatores irrigation_type (tipo de irrigação) e moisture (umidade) têm efeito estatisticamente significativo sobre a resposta AUDPC (p < 0,05 para ambos). Além disso, a interação entre tipo de irrigação e umidade também foi significativa (p < 0,05), indicando que o efeito de um fator depende do nível do outro. Esses resultados indicam que tanto a irrigação quanto a umidade influenciam de forma conjunta a severidade acumulada da doença ao longo do tempo.

Avaliação das premissas do modelo

Para verificar se os resíduos seguem uma distribuição adequada, usamos o pacote DHARMa:

plot(simulateResiduals(model_oidio))

Comparações múltiplas com `emmeans` e `cld`

medias_oidio <- emmeans(model_oidio, ~ moisture |
                          irrigation_type)

medias_oidio

irrigation_type = MS:
 moisture          emmean    SE df lower.CL upper.CL
 High moisture       8.52 0.223 12     8.04     9.01
 Moderate moisture  11.18 0.223 12    10.70    11.67

irrigation_type = MS above canopy:
 moisture          emmean    SE df lower.CL upper.CL
 High moisture       3.99 0.223 12     3.51     4.48
 Moderate moisture   4.86 0.223 12     4.37     5.34

irrigation_type = Overhead:
 moisture          emmean    SE df lower.CL upper.CL
 High moisture       3.68 0.223 12     3.20     4.17
 Moderate moisture   3.81 0.223 12     3.33     4.30

Confidence level used: 0.95

cld(medias_oidio)

irrigation_type = MS:
 moisture          emmean    SE df lower.CL upper.CL .group
 High moisture       8.52 0.223 12     8.04     9.01  1    
 Moderate moisture  11.18 0.223 12    10.70    11.67   2   

irrigation_type = MS above canopy:
 moisture          emmean    SE df lower.CL upper.CL .group
 High moisture       3.99 0.223 12     3.51     4.48  1    
 Moderate moisture   4.86 0.223 12     4.37     5.34   2   

irrigation_type = Overhead:
 moisture          emmean    SE df lower.CL upper.CL .group
 High moisture       3.68 0.223 12     3.20     4.17  1    
 Moderate moisture   3.81 0.223 12     3.33     4.30  1    

Confidence level used: 0.95 
significance level used: alpha = 0.05 
NOTE: If two or more means share the same grouping symbol,
      then we cannot show them to be different.
      But we also did not show them to be the same.

As médias ajustadas do AUDPC indicam diferenças na severidade acumulada entre os níveis de umidade dentro de cada tipo de irrigação. Para o tipo MS, a severidade foi significativamente maior na umidade moderada (11,18, grupo b) em comparação à alta umidade (8,52, grupo a), mostrando grupos estatísticos distintos. No tipo MS above canopy, também houve diferença significativa entre umidade moderada (4,86, grupo b) e alta (3,99, grupo a). Já no tipo Overhead, não houve diferença estatisticamente significativa entre os níveis de umidade, pois ambos compartilham a mesma letra de grupo (a).

GLM, ANOVA Fatorial e Interações: Aplicações Práticas no R

Diagnóstico com resíduos simulados (DHARMa)

Modelo de regressão linear generalizada (GLM) c com distribuição Poisson

Avaliação do modelo

Comparações múltiplas com emmeans e cld

Anova fatorial

Ajuste do modelo linear com interação

Análise de variância (ANOVA) do modelo ajustado

Avaliação do modelo

Comparações múltiplas com emmeans e cld

Avaliação da precisão do modelo

Análise de severidade da doença (OIDIO) com interação entre fatores

Modelo linear com interação

Avaliação das premissas do modelo

Comparações múltiplas com emmeans e cld

Comparações múltiplas com `emmeans` e `cld`

Comparações múltiplas com `emmeans` e `cld`

Comparações múltiplas com `emmeans` e `cld`